Introduction to NP Completeness
P and NP Problem
Introduction
In computer science, there exist several famous unresolved problems, and is one of the most studied ones. Until now, problems are not solved yet. We probably wonder why this problem is still not resolved.
In theoretical computer science, the classification and complexity of common problem definitions have two major sets;
which is “Polynomial” time and which “Non-deterministic Polynomial” time. There are also and sets, which we use to express more sophisticated problems. In the case of rating from easy to hard, we might label these as “easy”, “medium”, “hard”, and finally “hardest”:
- Easy : P
- Medium : NP
- Hard : NP Complete
- Hardest : NP Hard
P Problem
The class P consists of those problems that are solvable in polynomial time . e.g: O(n^k) here k=a constant and n is size of input.
these are basically tractable, they are solved by deterministic algorithms.
Examples
- A set of decision problem with yes/no answer.
- Calculating the greatest common divisor.
- sorting n numbers in ascending or descending order.
- search the element in the list
NP Problem

NP stands for non-deterministic polynomial time, it means verifiable in polynomial time.
the class NP consists of those problems that are justified in polynomial time.
if we were somehow given a certificate of a solution ,then we could verify that the certificate is correct in the polynomial time and the size of input.
A P-problem (whose solution time is bounded by a polynomial) is always also NP. If a problem is known to be NP, and a solution to the problem is somehow known, then demonstrating the correctness of the solution can always be reduced to a single P(polynomial time) verification. If P and NP are not equivalent, then the solution of NP-problems requires (in the worst case) an exhausting search.
Linear programming, long known to be NP and thought not to be P, was shown to be Pby L. Khachian in 1979. It is an important unsolved problem to determine if all apparently NP problems are actually P.
examples
- Knapsack problem
- Travelling salseman problem
- graph coloring problem
- hamiltonion circuit problem
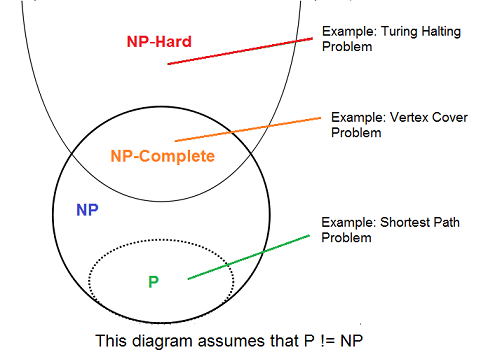
NP Hard and NP Complete problems
NP Complete Problem
A problem which is both NP and NP-hard is called an NP-complete problem
NP-complete problem, any of a class of computational problems for which no efficient solution algorithm has been found. Many significant computer-science problems belong to this class — e.g., the travelling salseman problem satisfiability problems, and graph-covering problems
L is NP-complete if
- L ϵ NP and
- L is NP-hard
If any NP-complete problem is solvable in polynomial time, then every NP-Complete problem is also solvable in polynomial time. Conversely, if we can prove that any NP-Complete problem cannot be solved in polynomial time, every NP-Complete problem cannot be solvable in polynomial time.
ex: knapsack problem ,lcs etc
NP Hard Problem
A problem is NP-hard if all problems in NP are polynomial time reducible to it, even though it may not be in NP itself.
Problem is NP-hard if for all L’ ϵ NP, L’ ≤p L. Thus if we can solve L in polynomial time, we can solve all NP problems in polynomial time.
NP problems are not only hard to solve but are hard to verify as well. In fact, some of these problems aren’t even decidable.
These algorithms have a property similar to NP- Complete Problems.
ex: K-means clustering , Knapsack problem
So , Does P=NP?

NOW P=NP ? is the biggest question which is still unsolved. to solve this you have to prove either way given below
1.if P=NP then give solution for the algorithm in NP solved by deterministic algorithm (means possible in theory as well as in practice)in polynomial time
2.if not then prove that the algorithm in NP will take minimum exponential time to solve and it can not be solved in polynomial time by using deterministic algorithm.
The problem in NP-Hard cannot be solved in polynomial time, until P = NP. If a problem is proved to be NPC, there is no need to waste time on trying to find an efficient algorithm for it. Instead, we can focus on design approximation algorithm.
so we can conclude that no one had proved this for all problems….
